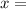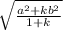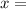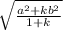Дана трапеция АВСD, ВС=а и АD=b, а < b, продолжим боковые стороны до пересечения в точке К. Получим 3 подобных треугольника КВС, КМN, KAD ( по 3 углам). Примем MN=x. Так как полощади подобных фигур относятся как квадраты их линейных размеров имеем: S(КВС):S(KMN):S(KAD)=a²:x²:b²
S(BCMN)=S(KMN)-S(KBC)
S(AMND)=S(KAD)-S(KMN)
Значит
S(BCMN)/S(AMND)=(x²-a²)/(b²-x²)=k
Отсюда найдем х:
х²-a²=kb²-kx²
x²+kx²=a²+kb²
x²(1+k)=a²+kb²
x²=(a²+kb²)/(1+k)