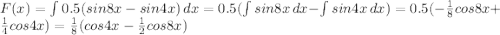Теплоход шёл 3 часа по течению и 4 часа против течения и проходит 348 км. За час по течению и 2 часа против течения теплоход проходит 148 км.

a/b

a^2-b^2=120

(a-1)/(b-1)=4/3

3(a-1)=4(b-1)

3а-3=4в-4

3а=4в-1

а=4/3 в - 1/3

(4/3 в - 1/3)^2- b^2 =120

16/9 b^2 - 2*4/3b*1/3+1/9-b^2=120

7/9 b^2-8/9 b+1/9=120|*9

7b^2-8b+1=1080

7b^2-8b-1079=0

D=64+4*7*1079=30276=174^2

b1=(8+174)/14=182/14=13      a1=4/3*13 - 1/3=51/3=17

b2=(8-174)/14=-166/14=-11.858  a2=4/3*(-11.858)-1/3=-16.145

Нам подходят значения а1 и в1

Проверка:

(17-1)/(13-1)=16/12=4/3

ответ: 17/13

Найдем частные производные и приравняем их 0 (необходимое условие экстремума).

z штрих по х = 2х + 2у - 4 = 0

z штрих по у = 2х + 4у - 4 = 0

Отсюда находим стационарную точку нашей ф-ии: х = 2; у = 0, или (2;0).

 Является ли эта точка экстремумом, и каким , если - да, определим из достаточных условий экстремума: А = z два штриха по х,х   = 2 больше 0.

В = z два штриха по х,у   = 2. С = z два штриха по у,у   = 4. 

Тогда определитель АС - В квадрат = 8-4=4 больше 0. И так как А тоже больше 0, имеем:

 точка (2,0) точка локального минимума ф-ии z(х,у) и он равен z нулевое = - 4 

1. 30%+25%=55%

2. 100%-55%=45%

3. 600км*45%=270км

на автобусе проехали  270 км

начало координат (0;0)

т.(0;0) удовлетворяет уравнению, значит

выполняется равенство

4*0-7*0=с

откуда с=0

ответ: с=0

например f(x)=корень квадратный (-х)

область определения -х>=0 или x<=0, т.е. данный луч

пусть костюм стоит х руб., тогда пальто стоит 1.7х рублей. По условию задачи

1.7х-х=59.5

0.7х=59.5

х=59.5\0.7

х=85

ответ: костюм стоит 85 рублей

1.

3x+y=10

x²-y=8

3x+x²=18

x²+3x-18=0

x²+6x-3x-18=0

x(x+6)-3(x+6)=0

(x-3)(x+6)=0

x=3 ∨ x=-6

3*3+y=10

9+y=10

y=1

3*(-6)+y=10

-18+y=10

y=28

(3,1),(-6,28)

3/4=0,75

Пусть а - число десятков исходного числа, а b - число единиц, тогда само исходное число равно 400+10а+b, новое же число равно 100а+10b+4 или 0,75(400+10а+b). Составим и решим уравнение:

100а+10b+4=0,75(400+10а+b)

100а+10b+4=300+7,5a+0,75b

100a-7,5a+10b-0,75b=300-4

92,5a+9,25b=296

9,25(10a+b)=296

10a+b=296:9,25

10a+b=32

Таким образом, в исходном числе 3 десятка и 2 единицы, а само число равно 432.

ответ: исходное число 432.

1. sin(a+b)+sin(a-b)=2sina cosb

sina*cosb+cosa*sinb+sina*cosb-cosa*sinb=2sina cosb

Воспользуемся формулой произведения синуса и косинуса:

sinx*cosy = 1/2 * (sin(x+y ) + sin (x-y)), тогда

sin2x*cos6x = 0.5*(sin8x+sin(-4x)) = 0.5*(sin8x-sin4x)

Запишем первообразную: