Математика
Математика из второго уравнения y=8/x
подставим вместо y полученное значение
x^2+(8/x)^2=65
x^2+64/(x^2)-65=0
умножим все на x^2
x^4-65x^2+64=0
сделаем замену z=x^2
z^2-65z+64=0
решив уравнение получим z1=1, z2=64
определим x и y
z1=1 ⇒ x1=1, y1=8
z1=1 ⇒ x2=-1, y2=-8
z2=64 ⇒ x3=8, y3=1
z2=64 ⇒ x4=-8, y4=-1
ответ: (1;8) (-1;-8) (8;1) (-8;-1)
 Алгебра
Алгебра  Алгебра
Алгебра  Алгебра
Алгебра Дана система уравнений: {x² - xy - y² = 3;
{2x²-xy- y² = 5.
Вычтем из второго уравнения первое: х² = 2. х = +-√2.
Подставим х = +√2 значение в первое уравнение.
2 - √2у - у² = 3.
у² + √2у + 1 = 0.
Квадратное уравнение, решаем относительно y:
Ищем дискриминант: D=(√)^2-4*1*1=2-4=-2;
Дискриминант меньше 0, уравнение не имеет корней.
Аналогичное решение при х = -√2.
ответ: система не имеет действительных корней.
 Алгебра
Алгебра 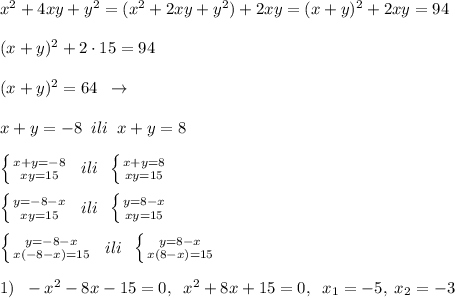
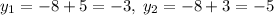
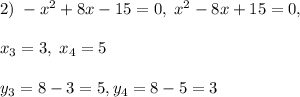
 Математика
Математика г) f(x) = 3x - tgx - 8, [0;π/4]
д) f(x) = 7sinx - 8x + 9, [-3π/2;0]
е) f(x) = 9x - 8sinx +7, [-π/2;0]
 Алгебра
Алгебра Два натуральных числа 16; 24.
Объяснение:
Найти два натуральных числа по заданным условиям.
Пусть первое число равно x, а второе равно y.
Тогда сумма их квадратов: x² + y² = 832,
а их произведение xy = 384.
Чтобы найти эти числа, решим систему уравнений.
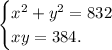
Умножим обе части второго уравнения системы на 2.

Сложим оба уравнения системы:
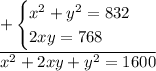
Свернем левую часть уравнения по формуле квадрата суммы двух выражений:
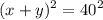
Получим следующую систему уравнений:
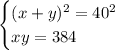
Извлечем квадратный корень из обеих частей первого уравнения.
С учетом того, что нам даны натуральные числа, получим следующую систему уравнений:
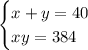
Выразим переменную y через x в первом уравнении и подставим полученное выражение во второе уравнение.
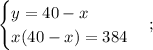
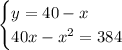
Решим второе уравнение системы.
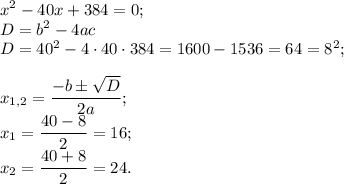
Тогда

Заданные натуральные числа 16 и 24.
 Алгебра
Алгебра  Алгебра
Алгебра решение во вложении
 Алгебра
Алгебра