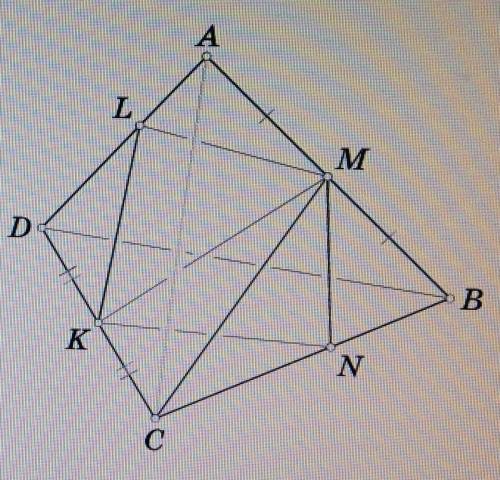
Пусть М и К - середины ребер АВ и СD тетраэдра ABCD.
Пусть плоскость, проходящая через М и К, пересекает ребра АD и ВС в точках L и N.
Плоскость DMC делит тетраэдр на 2 части равного объема, поэтому достаточно проверить, что равны объемы тетраэдров DKLM и CKNM.
Объем тетраэдра СКВМ равен 1/4 объема тетраэдра ABCD, а отношение объемов тетраэдров СКВМ и CKNM равно ВС:СN. Аналогично отношение 1/4 объема тетраэдра ABCD к объему тетраэдра DKLM равно AD:DL.
ВС:СN=AD:DL
 Геометрия
: задал doodndns4484
Геометрия
: задал doodndns4484 