Тело соскальзывает с наклонной плоскости с углом наклона 45 , коэффициент трения 0,2. найти ускорение

Физика

Шар массой 4 кг находится в ящике ,который соскальзывает по наклонной плоскости с углом наклона 45 градусов коэффициент трения равен 0,5 с какой силой шар давит на переднюю стенку

Пошаговый ответ

P Ответ дал Студент

Если считать что коробка не весомая то сила с которой шар давит на коробку будет равна силе реакции опоры стенки коробки которая в свою очередь равна силе трения действующей на ящик N = 13,87 H

Физика

Ящик массой 10 кг равномерно соскальзывает по наклонной плоскости с углом наклона 45 градусов. определить коэффициент трения скольжения.

Пошаговый ответ

P Ответ дал Студент

Если а=0, то tg(a)=M, где M-коэффициент трения.

tg45=1, следовательно M=1

Физика

Шайба, пущенная вверх по наклонной плоскости с углом наклона 45 градусов, со временем останавливается и соскальзывает вниз. время спуска в 2 раза больше времени подъема. определить коэффициент трения.

Пошаговый ответ

P Ответ дал Студент

2

ответ:

на шайбу дейтсвует вес, скатывающая сила и сила трения. скатывающая сила всегда направлена вниз взоль плоскости и равна вес умнодить на sin 45 град. сила трения в обоих случаях (шайба ещё скользит вверх или уже вниз) равна произведению реакции опоры на к-т трения. реакция опоры равна весу умножить на cos 45 град. прикол, однако, в том, что сила трения всегда направлена против движения. значит, пишем одно уравнение, что ускорение равно скатыващей силе плюс силе трения делить на массу, а второе - что ускорение равно скатывающей силе минус сила трения и тоже делитьна массу (масса в итоге сократится, так что можно просто обозначить м и забить). и сосчитать, сколько времени шайба будет с эти ускорением скользить вверх и вниз (путь в обоих случаях одинаковый, так чтотоже обозначить через s и тоже забить).

Физика

Вверх по наклонной плоскости с углом наклона к горизонту 45° пущена шайба со скоростью 12 м/с. через некоторое время она останавливается и соскальзывает вниз. с какой скоростью она вернется в исходную точку? коэффициент трения шайбы о плоскость 0,8.

Пошаговый ответ

P Ответ дал Студент

1) уравнение закона сохранения энергии для подъема шайбы:

(m v0²)/2 = mgh + Aтр, где Aтр - работа силы трения

v0² = 2gh + u gcosα S, где S - длина той части горки, по которой проехалась шайба. ее можно выразить как S = h / sinα. с учетом этого, получаем:

v0² = 2gh (1 + u ctgα),

откуда высота подъема шайбы равна:

h = v0² / 2g (1 + u ctgα).

2) уравнение закона сохранения энергии для спуска шайбы:

mgh = (m v²)/2 + Aтр.

аналогично выполняя преобразования, находим, что искомая скорость шайбы равна:

v = sqrt(2gh (1 - u ctgα).

с учетом выражения для h, получаем:

v = sqrt( (v0² (1 - u ctgα)) / (1 + u ctgα) ).

v = sqrt( 144*(1 - 0.6)/1.6) = 6 м/c

Физика

20 пружина находится в сжатом состоянии. чтобы сжать её еще на 2 см, необходимо выполнить работу 9,6 дж. найдите, на сколько сантиметров была сжата пружина изначально, если её жесткость составляет 12 кн/м. – 20 тело начинает соскальзывать с наклонной плоскости высотой 7 м и углом наклона 45°. его скорость в конце наклонной плоскости равна 9 м/с. найдите коэффициент трения тела о плоскость. решить , используя понятие полной механической энергии. – 20 шайба массой 160 граммов замедляется под действием силы трения со стороны льда. начальная скорость

Пошаговый ответ

P Ответ дал Студент

1. Составим по условию

к(х+0.02)²/2 - кх²/2=9.6,

0.04х+0.0004=19.2/(12*10³),

решаем: х=0.03м= 3см -ответ

Физика

Решить, нужно, . сколько можете (хоть одну). 1.мальчик, стоя на льду, пытается сдвинуть ящик за привязанную к нему веревку. масса ящика 90 кг, масса мальчика 45 кг. коэффициент трения ящика о лед 0,3, а мальчика 0,4. под каким минимальным углом к горизонту мальчик должен тянуть веревку, чтобы сдвинуть ящик? ответ округлить до целого числа градусов. 2.внутри откачанной до глубокого вакуума установки находится герметичный теплоизолированный цилиндрический сосуд, заполненный идеальным одноатомным газом. сосуд закрыт сверху теплонепроницаемым поршнем.

Пошаговый ответ

P Ответ дал Студент

Задача №7

1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)

2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).

Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.

3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:

Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t

Ox: v=0+g* cos a*t, то есть v=g*cos a*t

y=v0*t - g*sina*t^2/2 ; так как v0=g*sin a*t, то:

y = g*sina*t^2/2

x= g*cosa*t^2/2

4. s=√ y^2+x^2

s= (g*t^2/2) √ sin^2a+cos^2a , согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:

s= g*t^2/2

s=10*4*4/2=80(м)

ответ: 80 м

Решить, нужно, . сколько можете (хоть одну). 1.мальчик, стоя на льду, пытается сдвинуть ящик за прив

Физика

Чему равен коэффициент трения, если тело соскальзывает с наклонной плоскости высотой 2м и углом наклона 45, имея у основания скорость 6м/с ?

Пошаговый ответ

P Ответ дал Студент

Решение в изображении надеюсь поставите лучшее решение
можно решить решение через работу позволяет не рисовать силы
Чему равен коэффициент трения, если тело соскальзывает с наклонной плоскости высотой 2м и углом накл

Чему равен коэффициент трения, если тело соскальзывает с наклонной плоскости высотой 2м и углом накл

Физика

Тело начинает соскальзывать с наклонной плоскости высотой 7 м и углом наклона 45°. его скорость в конце наклонной плоскости равна 9 м/с. найдите коэффициент трения тела о плоскость. решить , используя понятие полной механической энергии.

Пошаговый ответ

P Ответ дал Студент

По идее так ................

Тело начинает соскальзывать с наклонной плоскости высотой 7 м и углом наклона 45°. его скорость в ко

Физика

Тело начинает соскальзывать с наклонной плоскости высотой 7 м и углом наклона 45°. его скорость в конце наклонной плоскости равна 9 м/с. найдите коэффициент трения тела о плоскость. решить , используя понятие полной механической энергии.

Пошаговый ответ

P Ответ дал Студент

Полная энергия вверху Е=Епот=mgh, она израсходована на кинетическую в конце и работу против сил трения по пути скольжения: Е=Екин+Атр. На основании з. сохранения полной энергии уравняем mgh=mv²/2+Fтр*S.
Длина пути S=h/sin(a), сила трения Fтр= k*mg*cos(a), тогда mgh=mv²/2+k*mg*h*ctg(a). При заданном ctg(45°)=1 получаем к=1-v²/(2gh) 1-9²/(20*7)=0.42. ответ к=0.42

Физика

Если есть добрая душа, то . три 1) тело соскальзывает с вершины наклонной плоскости высотой 8м и углом наклона 45 за 2с. определите коэффициент трения скольжения. начальная скорость тела равна нулю 2) небольшое тело скользит с вершины сферы вниз. на какой высоте от вершины тело оторвется от поверхности сферы? радиус сферы27 смтрение мало 3) на горизантальном участке полета с постоянной скоростью реактивный самолет выработал 7 т горючего и его импульс уменьшился в 1.5 раза определить в тоннах массу самолета в конце этого участка

Пошаговый ответ

P Ответ дал Студент

1. при движении бруска по наклонной плоскости соответствии со 2-м законом Ньютона:
mg+N+Fтр=ma
В проекциях на x(ось вдоль наклонной плоскости) и y(ось перпендикулярно ей) получаем
mgsinα – Fтр = ma
N – mgcosα = 0 ---> N= mgcosα
Fтр = µN = µmgcosα
тогда mgsinα - µmgcosα = ma
сократим на m: gsinα - µgcosα = a
µ = (gsina - a)/gcosa
ускорение равно а=2S/t^2
S(гипотенуза)=√ (2h^2) {так как угол 45)=√ 2*8:2=11.31
a=2*11.31/2^2=5.66 м/с2
тогда µ = (gsina - a ) /gcosa = (gsin45 - a)/gcos45 = 0.19

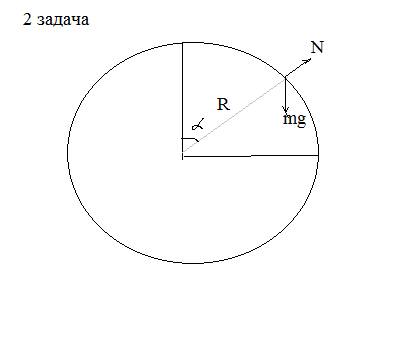
2. силы, действующие на скользящее тело: mg и N
в проекции на ось у
mgсosa(где a -угол поворота тела по сфере от начального положения) - N = ma
ускорение центростремительное а = v^2/R
чтобы тело оторвалось от поверхности, N=0
тогда mgcosa=mv^2/R
gcosa*R=v^2
по закону сохранения энергии mv^2/2=2gh
v^2=2gh
тогда gcosa*R=2gh
h=R*cosa/2
также h=R-Rcosa (по рисунку)
тогда Rcosa/2= R-Rcosa
cosa/2= 1-cosa
3cosa/2 = 1
cosa=2/3
тогда h = R-Rcosa= 27 - 27*2/3 = 9 см

3.по условию р1=1.5р2
р1=(M+mo)v - импульс ракеты в начале участка, М - масса ракеты без топлива, mo-масса израсходованного топлива, v - cкорость ракеты(постоянная)
р2=Mv - импульсракеты в конце участка
тогда (M+mo)v=1.5Mv
M+mo=1.5M
0.5M=mo
M=mo/0.5=7/0.5=14 т

Если есть добрая душа, то . три 1) тело соскальзывает с вершины наклонной плоскости высотой 8м и угл

Если есть добрая душа, то . три 1) тело соскальзывает с вершины наклонной плоскости высотой 8м и угл

Тело соскальзывает с наклонной плоскости с углом наклона 45', коэффициент трения 0,2. найти ускорение движения тела

Пошаговый ответ

Другие вопросы по предмету